LIDA objectives
Low-density parity-check error correction is a product of Bayesian reasoning. However, important aspects of iterative decoding are too complex to be described by probabilistic models. Unlike classical approaches, that use partial combinatorial and brute-force optimizations, we aim to design fast convergent iterative decoders with the help of learning techniques. The resulting decoders could be useful in energy-efficient cellular systems (5G and beyond), satellite communications systems, quantum communications, and data storage.
In the first activity, we analyzed the application of Deep Neural Networks (DNN) to improve iterative decoding algorithms for low-density parity-check codes. We have shown that a simpler configuration of DNNs cannot guarantee the performance of maximum likelihood decoding, with significantly lower complexity than trellis-based decoding. However, it can be an efficient post-processing block in decoding LDPC codes and lower error floors with a small complexity penalty.
Neural network
Our other aim was to optimize the gradient descent bit flipping (GDBF) decoder. By combining the concept of momentum and the graph properties of the typical trapping sets, we have proposed a deterministic modification of the GDBF algorithm with the new bit-flipping rule, based on the reliability information passed from neighboring nodes in the corresponding Tanner graph. The name Suspicion Distillation reflects the main feature of the algorithm - in every iteration we assign a level of suspicion to each variable node about its current bit value, and we introduce a concept of reliable and unreliable parity checks. In the course of iteration, we “distill” such suspicious bits and flip them. For short codes, this approach results in comparable performance compared with state-of-the-art belief propagation algorithm, with lower complexity.
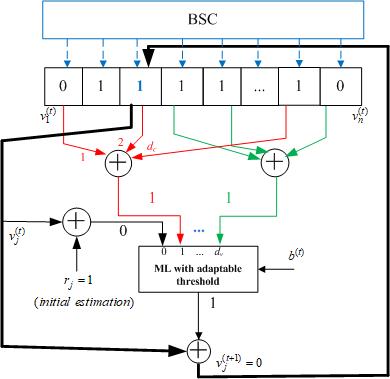
Gradient desscent bit-flipping decoder
